अंकगणित (Arithmetic) ही गणिताच्या सर्वात जुन्या आणि प्राथमिक शाखांपैकी एक आहे, जी ग्रीक शब्द ‘अरिथमॉस‘ पासून उद्भवली आहे, ज्याचा अर्थ ‘संख्या‘ आहे. ज्यामध्ये आपण विविध गुणधर्म वापरून संख्या आणि संख्यांमधील संबंधांचा अभ्यास करतो आणि उदाहरणे सोडवण्यासाठी त्यांचा वापर करतो. अंकगणितामध्ये संख्यांचा अभ्यास केला जातो, विशेषत: पारंपारिक ऑपरेशन्सचे गुणधर्म, जसे की: बेरीज (Addition) वजाबाकी (Subtraction) गुणाकार (Multiplication) विभागणी (Division)
या क्रियांवर आधारित अंकगणित ऑपरेटर ‘+’, ‘–’, ‘×’, आणि ‘÷’ आहेत. येथे अंकगणिताचे सर्व महत्त्वाचे विषय उदाहरणांसह जाणून घेऊया.

अंकगणित म्हणजे काय? (What is Arithmetic)
अंकगणित हे गणिताचे मूलभूत आहे. ज्यामध्ये संख्यांच्या क्रियांचा समावेश होतो. ही क्रिया बेरीज, वजाबाकी, गुणाकार आणि भागाकार आहेत. अंकगणित ही गणितातील एक महत्त्वाची शाखा आहे, जी विद्यार्थ्यांसाठी ‘गणित‘ या विषयाचा पाया घालते.
3+7×2 शिक्षकाने वर्गाला याचे मूल्य शोधण्यास सांगितले.
राम आणि श्याम हे उत्तर देणारे पहिले दोघे होते.
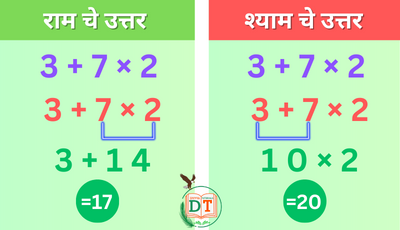
तुमच्या मते कोण बरोबर आहे?
राम ने, ते बरोबर समजले. त्याची गणना का बरोबर आहे आणि श्याम ने कोणती चूक केली हे समजून घेण्यासाठी पुढे बघूया. आम्ही असे करत असताना, आम्ही अंकगणित गणिताच्या विविध संकल्पना आणि त्यात समाविष्ट असलेल्या ऑपरेशन्सचा शोध घेऊ.
अंकगणिताचा इतिहास (History of Arithmetic)
1801 मध्ये कार्ल फ्रेडरिक गॉस यांनी संख्या सिद्धांताचे मूलभूत तत्त्व प्रदान केले होते, त्यानुसार, 1 पेक्षा जास्त असलेल्या कोणत्याही पूर्णांकाचे वर्णन केवळ एकाच पद्धतीने मूळ संख्यांचे गुणाकार म्हणून केले जाऊ शकते. अंकगणित हे संख्या सिद्धांताला दिलेले दुसरे नाव आहे. अंकगणितातील चार प्राथमिक क्रिया म्हणजे बेरीज, वजाबाकी, गुणाकार आणि भागाकार. या सर्व ऑपरेशन्सची आपण पुढे चर्चा करूया.
अंकगणिताचे मूलभूत नियम (Basic Rules of Arithmetic)
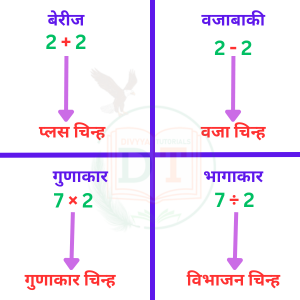
बेरीज आणि वजाबाकी (Addition and Subtraction)
बेरीज आणि वजाबाकी ही सर्वात मूलभूत अंकगणित क्रिया आहेत. या संकल्पना संख्या समजून घेण्याचे आणि कार्यान्वित करण्याचे घटक आहेत. आम्ही आमच्या दैनंदिन जीवनात संख्या, रक्कम आणि मूल्ये जोडतो आणि वजा करतो.
दोन किंवा अधिक प्रमाणांचे ‘एकत्र टाकणे‘ म्हणजे जोडणीची कल्पना केली जाऊ शकते.
अंकगणिताच्या गणितात वजाबाकी म्हणजे समूहातून काही गोष्टी काढून घेणे. दुसऱ्या शब्दांत, वजाबाकी ही समूहातून वस्तू काढून टाकण्याची प्रक्रिया आहे.
गुणाकार आणि भागाकार (Multiplication and Division)
गुणाकार हे चार मूलभूत अंकगणित क्रियांपैकी एक आहे जे भिन्न गणित संकल्पनांवर लागू केले जाऊ शकते जसे की अपूर्णांक (fractions), दशांश (decimals), परिमेय (rationals), पूर्णांक (integers), इ. या क्रिया गणिताच्या इतर संकल्पनांसाठी बिल्डिंग ब्लॉक्स बनवतात.
आणि मूलभूत अंकगणितातील शेवटची क्रिया म्हणजे भागाकार. सोप्या शब्दात, विभाजनाची व्याख्या मोठ्या गटाचे तितकेच लहान गटांमध्ये विभाजन म्हणून केली जाऊ शकते.
समान चिन्ह (Equal to Sign): “=“
अंकांवरील क्रियांचा परिणाम दर्शविण्यासाठी समान = चिन्हाचा वापर केला जातो.

reference – cuemath
उलट ऑपरेशन्स
ऑपरेशन्स बेरीज आणि वजाबाकी हे एकमेकांचे व्यस्त ऑपरेटर आहेत.
त्याचप्रमाणे, गुणाकार आणि भागाकाराची क्रिया एकमेकांचे व्यस्त ऑपरेटर आहेत.
जेव्हा आपण 3 ते 8 जोडतो तेव्हा आपल्याला 11 मिळतात. म्हणजे 8+3 = 11 याचा अर्थ असाही होईल.
- जर आपण 11 मधून 3 काढून घेतले तर आपल्याला 8 मिळेल.
- जर आपण 11 मधून 8 काढून घेतले तर आपल्याला 3 मिळेल.
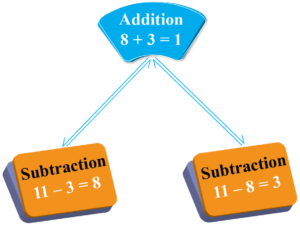
reference – cuemath
उदाहरण 2
3 चा 8 ने गुणाकार केल्याने 24 मिळते म्हणजे 8 x 3 = 24 याचा अर्थ असाही होईल.
- जर आपण 24 ला 3 ने भागले तर आपल्याला 8 मिळेल.
- जर आपण 24 ला 8 ने भागले तर आपल्याला 3 मिळेल.
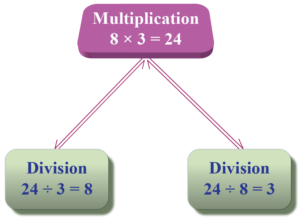
reference – cuemath
जेव्हा 1 पेक्षा जास्त ऑपरेटर उपस्थित असतात, तेव्हा त्यांना ऑपरेट करण्यासाठी DMAS नावाचा नियम असतो.

या नियमानुसार: जेव्हा आम्ही एकाधिक ऑपरेटरसह संख्या चालवतो, तेव्हा डावीकडून उजवीकडे जाताना आम्हाला प्रथम भागाकार किंवा गुणाकार आणि त्यानंतर ऑपरेटर बेरीज आणि वजाबाकीसह संख्या ऑपरेट करणे आवश्यक आहे.
आपण सुरुवातीला घेतलेले उदाहरण घेऊ,
3+7×2
येथे, आमच्याकडे 2 ऑपरेटर आहेत, गुणाकार आणि बेरीज.
तर, 7 आणि 2 चा पहिला गुणाकार केला जाईल आणि नंतर उत्तर 3 ला जोडले जाईल
Arithmetic operations (अंकगणित ऑपरेशन्स)
अंकगणित अंतर्गत मूलभूत ऑपरेशन्स बेरीज आणि वजाबाकी, भागाकार आणि गुणाकार आहेत, जरी या विषयामध्ये इतर अनेक सुधारित क्रियांचा समावेश आहे.
बेरीज (Addition) (+)
बेरीज ही अंकगणितातील मूलभूत क्रियांपैकी एक आहे. सोप्या फॉर्ममध्ये, बेरीज दोन किंवा अधिक मूल्यांना एकाच शब्दात एकत्रित करते, उदाहरणार्थ 2 + 5 = 7, 6 + 2 = 8, जेथे ‘+’ हा जोड ऑपरेटर आहे.
दोनपेक्षा जास्त मूल्ये जोडण्याच्या प्रक्रियेला समीकरण म्हणतात आणि त्यात मूल्यांची संख्या जोडण्याच्या पद्धतींचा समावेश होतो.
जोडणीचा ओळख घटक 0 आहे, याचा अर्थ कोणत्याही मूल्यामध्ये 0 जोडल्यास समान परिणाम मिळतो. बेरीजचा व्यस्त घटक हा कोणत्याही मूल्याच्या विरुद्ध असतो, याचा अर्थ असा की अंकामध्ये कोणत्याही अंकाच्या विरुद्ध गुण जोडल्याने बेरीजची ओळख मिळते. उदाहरणार्थ,
5 च्या विरुद्ध –5 आहे, म्हणून 5 + (-5) = 0.
जोडण्याची उदाहरणे
8 + 10 = 18
12 + 5 = 17
वजाबाकी (Subtraction) (-)
वजाबाकीला जोडण्याचे व्यस्त असे लेबल केले जाऊ शकते. हे दोन मूल्यांमधील फरकाची गणना करते, उदा. वजाबाकीचा ऑपरेटर ‘–‘ आहे.
उदाहरणार्थ
4 – 3 = 1
3 – 4 = -1
गुणाकार (Multiplication) (×)
गुणाकार देखील एकल मूल्य किंवा उत्पादनामध्ये बेरीज आणि वजाबाकी या दोन मूल्यांना एकत्र करते. दोन मूळ मूल्ये गुणाकार आणि गुणक म्हणून ओळखली जातात किंवा फक्त दोन्ही घटक म्हणून ओळखली जातात.
a आणि b चे गुणाकार a·b किंवा a × b असे व्यक्त केले जाते, जेथे ‘×’ हा गुणाकार ऑपरेटर आहे. सॉफ्टवेअर भाषांमध्ये ज्यामध्ये फक्त कीबोर्डमध्ये आढळणारी अक्षरे वापरली जातात, ती सहसा a*b (* याला तारांकन म्हणतात) म्हणून व्यक्त केली जाते.
उदाहरणार्थ
4 × 5 = 20
2 × 3 = 6
विभाग (Division) (÷)
भागाकार हा गुणाकाराचा व्यस्त आहे. विभागणी पद्धतीसाठी वापरलेला ऑपरेटर कधीकधी ‘÷’ किंवा ‘/’ असतो. हे दोन संख्यांच्या भागांकाची गणना करतात.
भाग 1 पेक्षा जास्त आहे जर लाभांश कोणत्याही चांगल्या-परिभाषित सकारात्मक संख्येसाठी विभाजकापेक्षा जास्त असेल तर तो 1 पेक्षा लहान असेल.
उदाहरणार्थ
10 ÷ 2 = 5
9 ÷ 3 = 3
अंकगणित क्रम म्हणजे काय? (What is Arithmetic Sequence?)
अंकगणितीय क्रम हा संख्यांचा क्रम असतो, जेथे एक पद आणि पुढील पदांमधील फरक स्थिर असतो. उदाहरणार्थ, 1, 4, 7, 10, 13, 16, 19, 22, 25, … हा 3 च्या समान फरकासह एक अंकगणितीय क्रम आहे. याला अंकगणित प्रगती असेही म्हणतात आणि सामान्यतः असे दर्शविले जाते:
a, a + d, a + 2d, a + 3d, a + 4d, ………. ,a + (n – 1) d
a = पहिली मुदत
d = अटींमधील सामान्य फरक
n = पदांची संख्या
अंकगणित सोडवलेल्या समस्या (Arithmetic Solved Problems)
प्रश्न 1: दोन संख्यांची बेरीज 50 आहे आणि त्यांच्यातील फरक 30 आहे. संख्या शोधा.
उपाय: संख्या x आणि y असू द्या. आता दिलेल्या परिस्थितीनुसार,
x + y = 50……………………(i)
आणि x – y = 30………………(ii)
आपण x = 50-y, eq.(i) वरून लिहू शकतो.
म्हणून, x चे मूल्य eq (ii) मध्ये टाकल्यास, आपल्याला मिळेल,
50 – y – y = 30
50 -2y = 30
2y = 50-30= 20
y = 20/2 = 10
आणि x = 50 – y = 50-10 = 40
म्हणून, दोन संख्या 40 आणि 10 आहेत.
प्रश्न 2 : 25 + 5 (27 ÷ 3) – 9 सोडवा.
उपाय: 25 + 5(27 ÷ 3) – 9
- 25 + 5(9) – 9
- 25 + 45 – 9
- 70 – 9 = 61
अंकगणितावरील प्रश्नांचा सराव करा.
सोडवा: 4 + 3 x 10 – 1
सोडवा: 246 x 132
सोडवा: 9/10 – 3/20
65 म्हणजे 500 च्या किती टक्के?


